Here we will solve LeetCode problem “34. Find First and Last Position of Element in Sorted Array“. The problem statement is as below:
Given an array of integers nums sorted in non-decreasing order, find the starting and ending position of a given target value. If target is not found in the array, return [-1, -1]. You must write an algorithm with O(log n) runtime complexity.
Input: nums = [1, 1, 3, 3, 7, 8, 9]target = 3Output: [2, 3]
We can easily find a particular element in a sorted array using binary search. That would take O(log n) time complexity only. But here we can have same element multiple times. And we need to find the range for that target element. One way to do this would be to do a binary search. We will get one instance of that element. Now we can go to the left hand side one by one till the element matches the target value. That way we will find leftmost element. Same we can do for the rightmost element. But let us consider an input array of [3, 3, 3, 3, 3, 3, 3, 3] & target value of 3. We will find the middle element with value 3. Now we would have to go to the left side till the first position of the array. And in right side, we would have to go to the end of the array. If we do that one by one, we would traverse all n elements. So worst time complexity would be O(n).
So how can we keep worst time complexity as O(log n)? We will use a modified version of binary search. To find leftmost & rightmost values, we will run two binary searches separately.
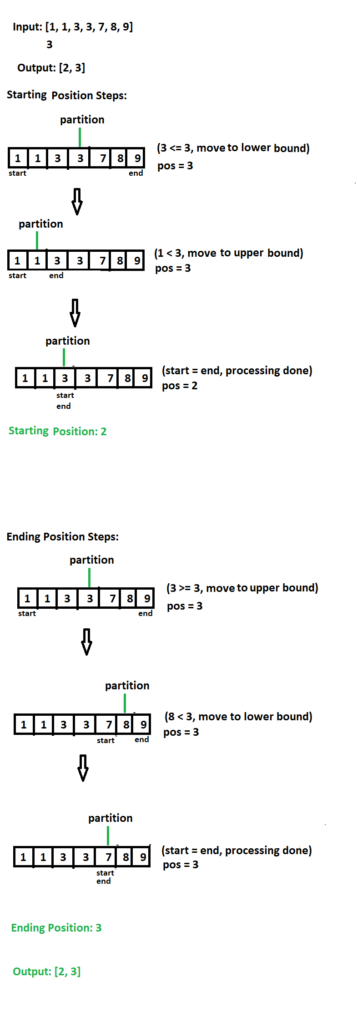
For leftmost target, we will move towards lower bound when target is less than or equal to the current element. We will move to upper bound in case target is greater than the current element. And we will keep a separate variable to track the last found position of the target. We will run the loop till (lower bound >= upper bound). As we move to lower bound even when there is a match, we are looking for same target again in lower part. We will get the leftmost element that way. You can find the steps in the diagram above. The visual should be intuitive.
For rightmost target, we will move towards lower bound when target is less than the current element. But we will move to upper bound in case target is greater than or equal to the current element. As we move to upper bound when there is a match & run the loop till (lower bound >= upper bound), we will find the rightmost element. The diagram should be helpful to understand this.
We are running two binary searches. So worst time complexity is (log n + log n = 2 log n) or O(log n). This way we can find starting position & ending position of the target value in O(log n) time complexity.
The fully working Java code solution is given below.
class Solution {
public int[] searchRange(int[] nums, int target) {
int leftPos = findLeftMost(nums, target);
int rightPos = findRightMost(nums, target);
int[] result = new int[2];
result[0] = leftPos;
result[1] = rightPos;
return result;
}
private int findLeftMost(int[] nums, int target){
int pos = -1;
int lowerBound = 0;
int upperBound = nums.length - 1;
while(upperBound >= lowerBound){
int mid = lowerBound + ((upperBound - lowerBound)/ 2);
if(target <= nums[mid]){
if(nums[mid] == target){
pos = mid;
}
upperBound = mid - 1;
} else {
lowerBound = mid + 1;
}
}
return pos;
}
private int findRightMost(int[] nums, int target){
int pos = -1;
int lowerBound = 0;
int upperBound = nums.length - 1;
while(upperBound >= lowerBound){
int mid = lowerBound + ((upperBound - lowerBound) / 2);
if(target >= nums[mid]){
if(nums[mid] == target){
pos = mid;
}
lowerBound = mid + 1;
} else {
upperBound = mid - 1;
}
}
return pos;
}
}