Here we will understand a common problem solving question from LeetCode. It is “239. Sliding Window Maximum”.
You are given an array of integers nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position. Return the max sliding window.
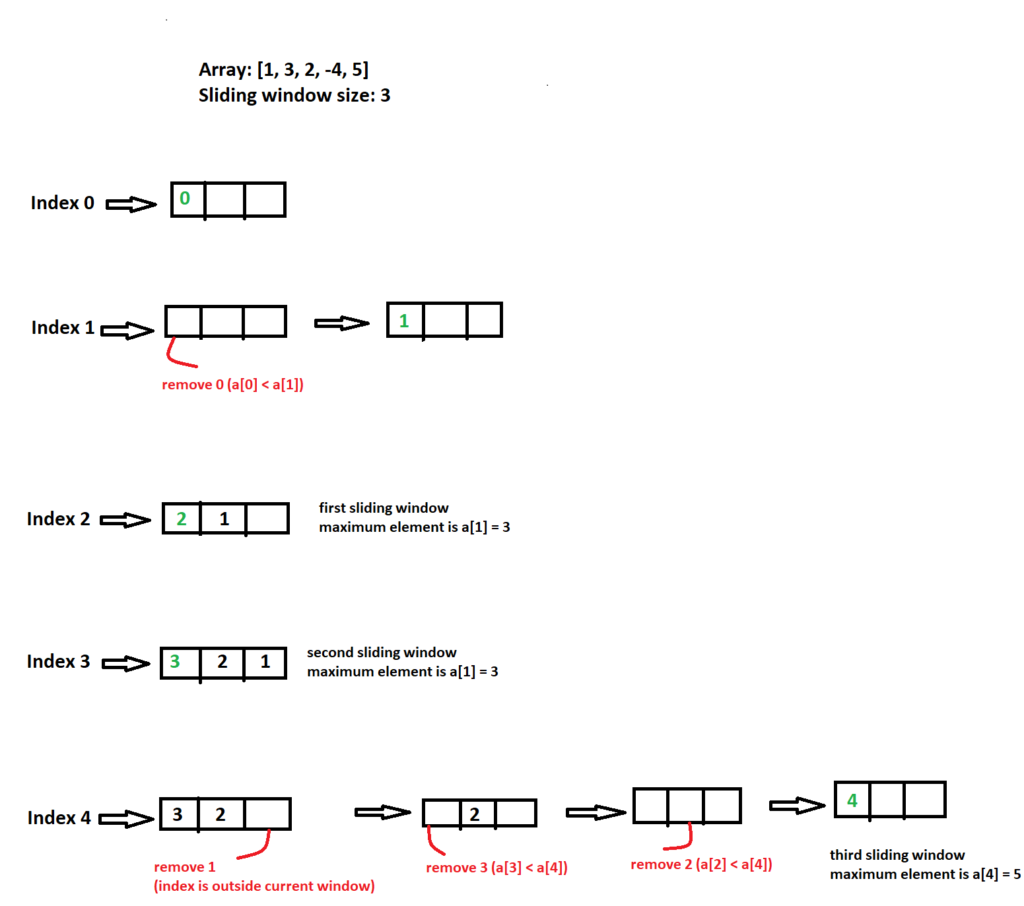
Input: nums = [1, 3 , 2, -4, 5], k = 3 Output: [3, 3, 5] Window position Max --------------- ----- [1 3 2] -4 5 3 1 [3 2 -4] 5 3 1 3 [2 -4 5] 5
Let’s consider array length as n & sliding window length as m. We can solve this problem brute-force way using one outer loop & one inner loop. First loop will iterate from 1 to n one by one. For each iteration, we will have an inner loop. Inner loop will iterate from current outer loop position till m elements. Inside inner loop, we will track the largest value. That will be the maximum element for that window. Time complexity would be O(n * m).
How can we optimize the solution to achieve a linear time complexity? We can do that with the help of deque data structure. Deque or double ended queue is a data structure which supports both queue & stack functionalities. Basically we can add & remove elements from both front & rear of deque in O(1) time. We will store index of the array elements in the deque.
- The plan is to store indexes of elements for the current window only.
- We will store & keep indexes in such a way that corresponding values will be in descending order. Then the first entry in deque will always have the maximum value.
To achieve above two points, we need to follow below steps while inserting an index in the deque:
- Before inserting new index, delete first entry from deque if the entry falls outside of current sliding window index range.
- Before inserting new index, read & remove any last entry in the deque whose value is less than the new element value. This way, we can make sure that inserted indexes are always in descending order of their values. We can remove any smaller entry from the deque as we are only concerned about the maximum one.
You can check the below diagram to figure out how we implemented above steps.
Overall Time Complexity:
Point 1 takes O(1) time as we are getting first entry from the front of deque.
Point 2 also takes O(1) time. We are removing entries from rear of deque. Entries can be added & removed only once. Also there can be maximum one extra comparison when last deque value is greater than new element value. So no operation depends on m or n.
We are traversing n elements. So time complexity of above solution would be O(n). That is linear time complexity.
Here is the fully working Java code solution of the above LeetCode problem.
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int[] results = new int[nums.length - k + 1];
int currentResultIndex = -1;
if(k > nums.length){
int slidingMaximum = 0;
for(int num : nums){
if(slidingMaximum < num){
slidingMaximum = num;
}
}
results[++currentResultIndex] = slidingMaximum;
return results;
}
LinkedList<Integer> deque = new LinkedList<Integer>();
for(int i = 0; i < k; i++){
while(!deque.isEmpty() && nums[deque.getLast()] <= nums[i]){
deque.removeLast();
}
deque.addLast(i);
}
for(int i = k; i < nums.length; i++){
results[++currentResultIndex] = nums[deque.getFirst()];
while(!deque.isEmpty() && deque.getFirst() <= (i-k)){
deque.removeFirst();
}
while(!deque.isEmpty() && nums[deque.getLast()] <= nums[i]){
deque.removeLast();
}
deque.addLast(i);
}
results[++currentResultIndex] = nums[deque.getFirst()];
return results;
}
}