Should I write an article explaining Merge Sort? There are tons of articles or videos online which explain Merge Sort. What new am I going to add? This is what I thought initially. But after a bit of hesitation, I have decided to write a post on Merge Sort. I would try to explain it in simple terms without any jargon. Hopefully it would be helpful for beginners.
We will try to understand Merge Sort using a concrete example.
Input: 12 30 25 33 8 Output: 8 12 25 30 33
We have an array of 5 integers [12, 30, 25, 33, 8]. We need to sort this unsorted array. Merge Sort does the sorting in two distinct phases.
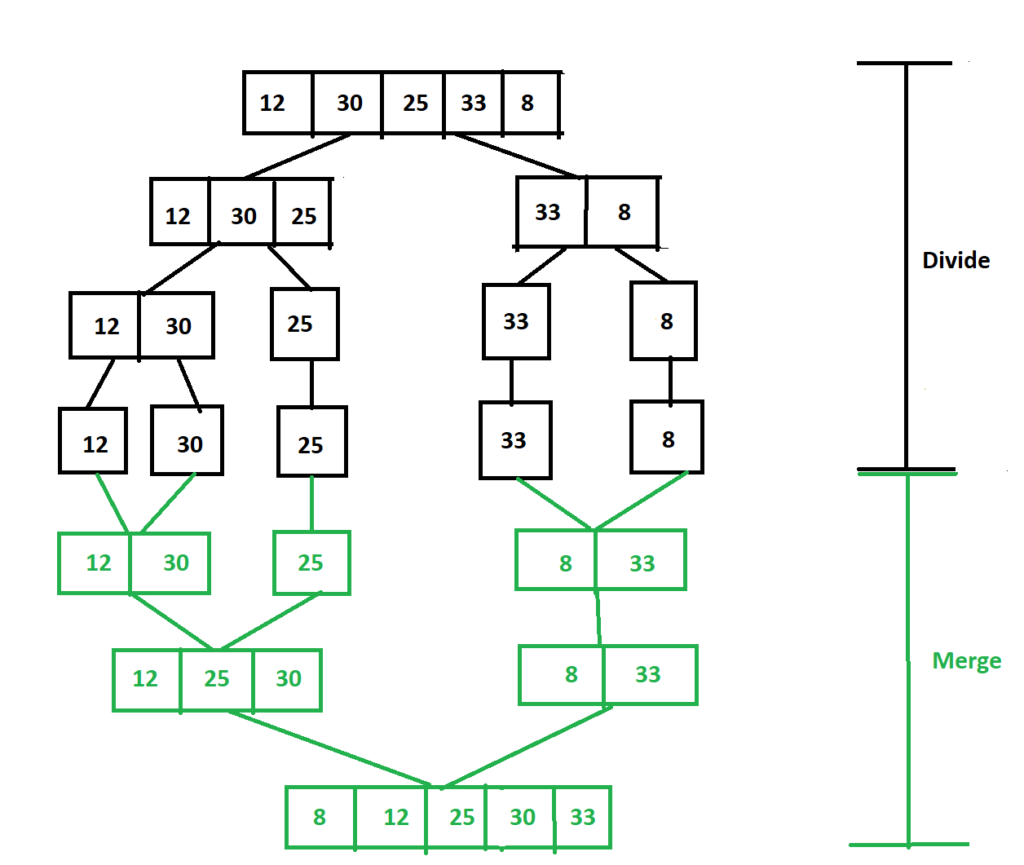
Divide Phase: First we will divide the unsorted array in two equal halves. Let’s say in our case these are [12, 30, 25] & [33, 8]. Merge Sort will keep on dividing each of these sub-arrays in equal halves till each sub-array has only one element. Once we reach a state where each array contains only single element, we will stop dividing. But why does Merge Sort stop dividing at this point? And how does divide phase help in sorting? If we think a bit, an array with a single element is already sorted, there is nothing more to sort. By doing this, Merge Sort converted the initial problem of sorting an unsorted array of 5 elements to a different problem. Now the problem is that we need to merge 5 sorted arrays into a single sorted array.
Merge Phase: Merging of already sorted arrays is comparatively easier than sorting an unsorted array. If you see the diagram, each recursive call has at most two sorted arrays which need to be merged. Merging of already sorted arrays to a single sorted array can be done in linear time complexity. For two arrays scenario, we can have two pointers pointing to the initial positions of the arrays. At each loop iteration, we will compare current elements of the two arrays, add smaller element to the result array & increment the corresponding counter. So worst time complexity would be array1 length + array2 length. Java code for merging logic is given at the bottom of the post.
I think the purpose of these two steps are clear now. Divide phase prepares the input for merging phase. Merging phase actually arranges the elements in a sorted manner. As we discussed, the time complexity of merging is linear. In a recursion level, merging would happen for total n elements. So time complexity of merging in a single recursion level is O(n). Now what is the total number of recursion levels where merging actually takes place? It would be same as the maximum height of the recursion tree. To find the height of recursion tree, we need to relook into the divide phase. Divide phase keeps on splitting the array into two equal halves until we reach to single element arrays. Let’s say recursion tree height is h & number of elements in the array is n.
2 ^ 0 + 2 ^ 1 + ... + 2 ^ (h - 1) + 2 ^ h = n2 ^ (h + 1) - 1 = n2 ^ (h + 1) = n + 1h + 1 = log base 2 (n + 1)h = log (n + 1) - 1
As we can see from above calculation, total number of recursion levels where merging takes place is log (n + 1) – 1. And we know that merging for a single recursion level takes O(n) time. So we can say worst time complexity of Merge Sort is O(n log n). The diagram above should be intuitive in understanding the time complexity.
Here is the fully working solution of Merge Sort in Java. This same code can be used as a solution for LeetCode problem “912. Sort an Array”.
class Solution {
public int[] sortArray(int[] nums) {
mergeSort(nums, 0, nums.length - 1);
return nums;
}
void merge(int arr[], int l, int m, int r) {
int[] leftArr = new int[m - l + 1];
int[] rightArr = new int[r - m];
for(int i=l; i<= m; i++){
leftArr[i-l] = arr[i];
}
for(int i=m+1; i<=r; i++){
rightArr[i-(m+1)] = arr[i];
}
int x = 0;
int y = 0;
int i = l;
while(x < leftArr.length && y < rightArr.length){
if(leftArr[x] > rightArr[y]){
arr[i] = rightArr[y];
y++;
} else {
arr[i] = leftArr[x];
x++;
}
i++;
}
while(x < leftArr.length){
arr[i] = leftArr[x];
x++;
i++;
}
while(y < rightArr.length){
arr[i] = rightArr[y];
y++;
i++;
}
}
void mergeSort(int arr[], int l, int r) {
if(l >= r){
return;
}
int m = l + (r-l) / 2;
mergeSort(arr, l, m);
mergeSort(arr, m+1, r);
merge(arr, l, m, r);
}
}